Deep Learning的本质是多层的神经网络,因此在深入学习Deep Learning之前,有必要了解一些神经网络的基本知识。 本文首先对神经网络的发展历史进行简要的介绍,然后给出神经元模型的形式化描述,接着是神经网络模型的定义、特性, 最后是一些最新的进展等。关于神经网络的分类、学习方法、应用场景等将在后续文章中介绍。
1.发展简史
1943年,心理学家W.S.McCulloch和数理逻辑学家W.Pitts建立了神经网络和数学模型,称为MP模型。他们通过MP模型提出 了神经元的形式化数学描述和网络结构方法,证明了单个神经元能执行逻辑功能,从而开创了人工神经网络研究的时代。 1945年,Von Neumann在成功的试制了存储程序式电子计算机后,他也对人脑的结构与存储式计算机进行的根本区别的比较,还提出了以简单神经元构成的自再生自动机网络结构。 1949年,心理学家D.O.Heb提出了突触联系强度可变的设想,并据此提出神经元的学习准则——Hebb规则,为神经网络的学习算法奠定了基础。 1958年,F.Rosenblatt提出了感知模型,该模型是由阈值神经元组成的,它试图模拟动物和人的感知和学习能力。 1962年Widrow提出了自适应线性元件,这是一种连续的取值的线性网络,主要用于自适应信号处理和自适应控制。
Minkey和Papert从数学上对感知机的功能及其局限性做了深入的分析,于1969年出版了《Perceptron(感知机)》一书, 提出感知机不可能实现复杂的逻辑函数,他们认为感知机的功能是有限的,不能解决如XOR这样的基本问题,而且多层的 网络还不能找到有效的计算方法,进而否定了这一模型。(其实在后来发现,加入隐藏层就可以解决XOR问题。) 虽然冯诺依曼结构和感知机结构大概是一个历史阶段的产物,由于《Perceptron》一书的悲观情绪和冯诺依曼机的快速发展, 神经网络进入了低潮。直到1982年Hopfield提出了HNN模型,他引入了“计算能量函数”的概念,给出了网络稳定性的判据, 推动了人工神经网络技术得以发展。特别是他提出的电子电路的实现为神经计算机的研究奠定的基础。 1986年,Rumelhart及LeCun等学者提出了多层感知器的反向传播算法,克服了当初阻碍感知机继续发展的重要障碍。 与此同时,冯诺依曼机在处理视觉、听觉、联想记忆都方面都体现出了局限性,促使人们开始寻找更加接近人脑的 计算模型,于是又产生了对神经网络研究的热潮。 目前,神经网络的发展非常迅速,从理论上对它的计算能力、对任意连续函数的逼近能力、学习理论以及动态网络的 稳定性分析上都取得了丰硕的成果。特别是在应用上已迅速扩展到许多重要领域,如模式识别与图像处理中的手写体 字符识别,语音识别,人脸识别,基因序列分析,控制及优化,;金融中的股票市场预测,借贷风险管理,信用卡欺骗检测等。
2 神经元模型
2.1概述
神经网络的基本组成单元是神经元,在数学上的神经元模型是和在生物学上的神经细胞对应的,也就是说,人工神经网络理论是 用神经元这种抽象的数学模型来描述客观世界的生物细胞的。因此,生物的神经细胞是神经网络理论诞生和形成的物质基础和源泉。 这样,神经元的数学描述就必须以生物神经细胞的客观行为特性为依据。本节在介绍了生物神经元的基本结构的基础上,给出了神经元 的数学模型和形式化表示。
2.2生物神经元
生物神经元是大脑处理信息的基本单元,人脑大约由1011个神经元组成,神经元互相连接成神经网络。神经元以细胞体为主体, 由许多向周围延伸的不规则树枝状纤维构成的神经细胞,其形状很像一棵枯树的枝干。主要由细胞体、树突、轴突和突触(Synapse, 又称神经键)组成,如图1所示。
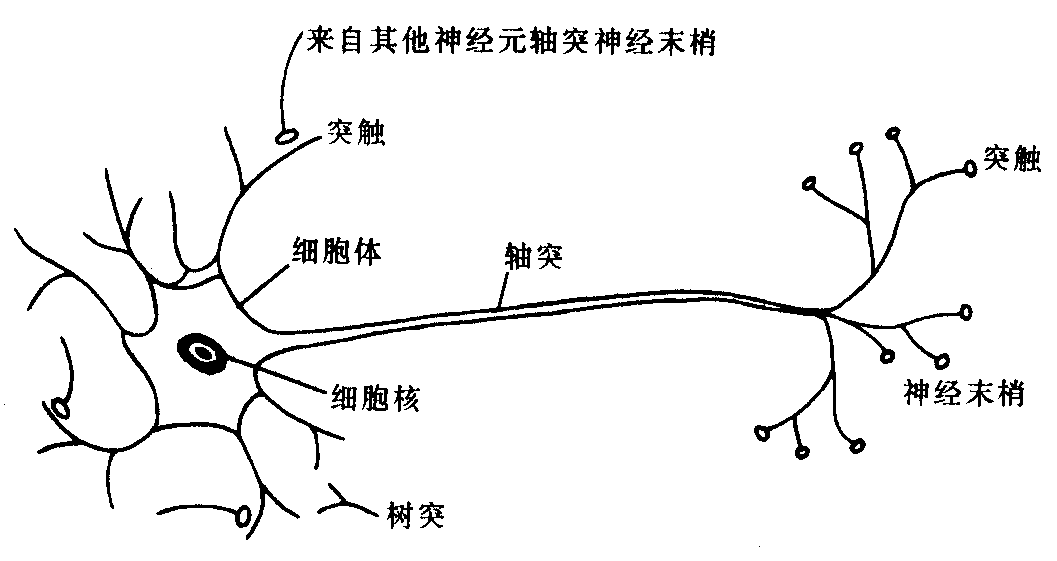
2.3人工神经元模型
神经元是神经网络中最基本的信息处理单元,其形式化表示如图2所示。
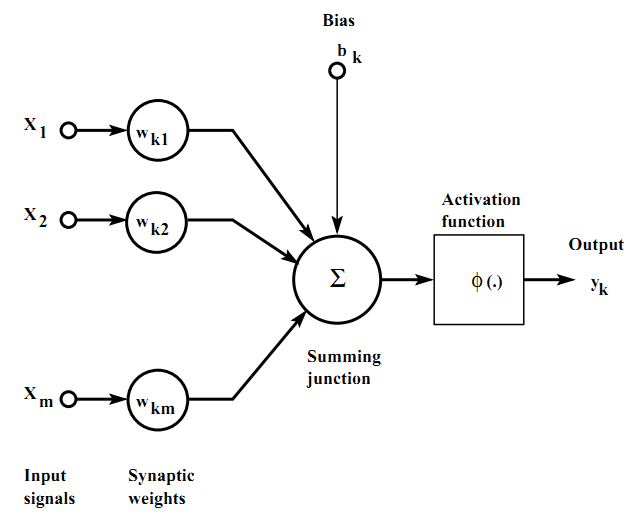
一个典型的神经元模型由以下3个部分组成: 1)突触集(a set ofsynapses):用权重(weights)来表示。 2)加法器(adder):将加权后的输入进行求和,即$\sum_{j=1}^{n} w_{kj} x_{j}$ 3)激活函数(activation function):也称为压缩函数(squashing function),作用于神经元的输出,一般是一个非线性函数,常见的有。 另外,很多时候一个神经元还包含一个偏置项bk。 可用用如下的数学表达式来刻画一个神经元:
其中,$u_{k}$表示输入的线性加和,$\varphi (·)$表示激活函数,$y_{k}$表示神经元的输出,$x_{i}$表示输入信号,$w_{ki}$表示权重。 很多时候,为了表示的简单,在输入中加入$x_{0}$项、权重中加入$w_{k0}$项,将偏置$b_{k}$表示为$x_{0} * w_{k0}$。
3. 神经网络模型及其特性
3.1概念
神经网络(Neural Networks,NN)是由大量的、简单的处理单元(称为神经元)广泛地互相连接而形成的复杂网络系统,它反映了人脑功能的 许多基本特征,是一个高度复杂的非线性动力学习系统。一个典型的神经网络结构如图3所示。这是一个多层的(包含两个隐层L2、L3)、包含两个 输出单元的神经网络拓扑结构。
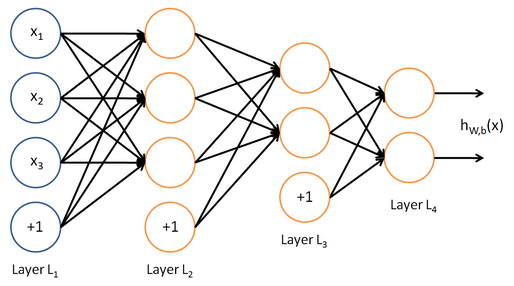
人工神经网络(Artificial Neural Network,ANN)结构和工作机理基本上是以人脑的组织结构(大脑神经元网络)和活动规律为背景的, 它反映了人脑的某些基本特征,但并不是要对人脑部分的真实再现,可以说它是某种抽象、简化或模仿。
3.2基本特性
神经网络具有四个基本特征:
(1)非线性
非线性关系是自然界的普遍特性。大脑的智慧就是一种非线性现象。人工神经元处于激活或抑制二种不同的状态,这种行为在数学上表现 为一种非线性关系。具有阈值的神经元构成的网络具有更好的性能,可以提高容错性和存储容量。
(2)非局限性
一个神经网络通常由多个神经元广泛连接而成。一个系统的整体行为不仅取决于单个神经元的特征,而且可能主要由单元之间的相互作用、 相互连接所决定。通过单元之间的大量连接模拟大脑的非局限性。联想记忆是非局限性的典型例子。
(3)非常定性
人工神经网络具有自适应、自组织、自学习能力。神经网络不但处理的信息可以有各种变化,而且在处理信息的同时,非线性动力系统本身 也在不断变化。经常采用迭代过程描写动力系统的演化过程。
(4)非凸性
一个系统的演化方向,在一定条件下将取决于某个特定的状态函数。例如能量函数,它的极值相应于系统比较稳定的状态。非凸性是指这种 函数有多个极值,故系统具有多个较稳定的平衡态,这将导致系统演化的多样性。
4.近期进展
最近几年神经网络模型又成了研究热点,这是因为深层神经网络的学习方法取得了突破性的成就。2006年,以Hinton为首的研究人员在深度置信 网络(Deep Belief Networks,DBNs)方面的划时代性的工作,极大的减小了深层神经网络的训练和测试误差,从此深度学习的方法一路所向披靡, 在交通路标识别、字符识别、人脸识别、语音识别等方面的顶级Contest中都取得了最佳效果。
值得一提的是,谷歌的“Google Brain”项目,使用16000个PC机,从YouTube视频中找到的1000万张数字照片作为训练数据集, 用非监督学习的方法建立了一个拥有10亿多条连接的深层神经网络,最后成功的从中识别出猫咪的图片。
参考文献
[1] Simon Haykin, “Neural Networks: a Comprehensive Foundation”, 2009 (3rd edition) [2]T-61.3030 PRINCIPLES OF NEURAL COMPUTING (5 CP) [3] Wiki - Neural network: http://en.wikipedia.org/wiki/Neural_network [4] 百度百科-神经网络模型:http://baike.baidu.com/view/3406239.htm [5] 人工神经网络综述:http://ishare.iask.sina.com.cn/f/36537774.html [6] How bio-inspired deep learning keeps winning competitions:http://www.kurzweilai.net/how-bio-inspired-deep-learning-keeps-winning-competitions [7] Google's 'brain simulator': 16,000 computers to identify a cat:http://www.smh.com.au/technology/sci-tech/googles-brain-simulator-16000-computers-to-identify-a-cat-20120626-20zmd.html