反向传播(BP)神经网络

前面几篇文章中对神经网络和深度学习进行一些简介，包括神经网络的发展历史、基本概念和常见的几种神经网络以及神经网络的学习方法等， 本文具体来介绍一下一种非常常见的神经网络模型——反向传播(Back Propagation)神经网络。

1.概述

BP（Back Propagation）神经网络是1986年由Rumelhart和McCelland为首的科研小组提出，参见他们发表在Nature上的论文 Learning representations by back-propagating errors 值得一提的是，该文的第三作者Geoffrey E. Hinton就是在深度学习邻域率先取得突破的神犇。

BP神经网络是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的 输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断 调整网络的权值和阈值，使网络的误差平方和最小。

2.BP网络模型

一个典型的BP神经网络模型如图1所示。

图1 典型的BP神经网络模型

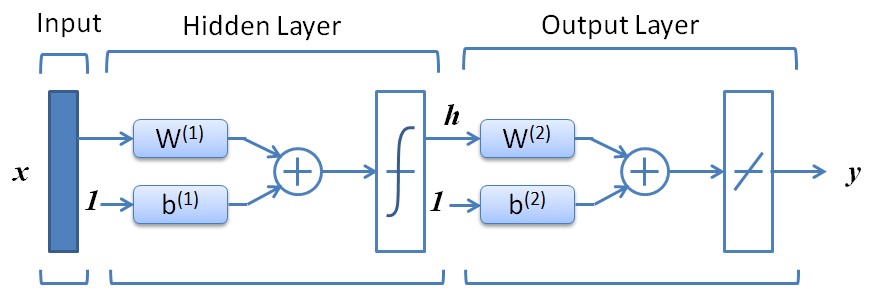
BP神经网络与其他神经网络模型类似，不同的是，BP神经元的传输函数为非线性函数(而在感知机中为阶跃函数，在线性神经网络中为线性函数)，最常用的 是log-sigmoid函数或tan-sigmoid函数。BP神经网络(BPNN)一般为多层神经网络，图1中所示的BP神经网络的隐层的传输函数即为非线性函数，隐层可以有多层， 而输出层的传输函数为线性函数，当然也可以是非线性函数，只不过线性函数的输出结果取值范围较大，而非线性函数则限制在较小范围（如logsig函数输出 取值在(0,1)区间）。图1所示的神经网络的输入输出关系如下：
1)输入层与隐层的关系：

$\boldsymbol{h} = \mathit{f_{1}} (\boldsymbol{W^{(1)}x}+\boldsymbol{b^{(1)}})$. 其中$\boldsymbol{x}$为$m$维特征向量(列向量)，$\boldsymbol{W^{(1)}}$为$n × m$维权值矩阵，$\boldsymbol{b^{(1)}}$为$n$维的偏置(bias)向量(列向量)。
2)隐层与输出层的关系：
$\boldsymbol{y} = \mathit{f_{2}} (\boldsymbol{W^{(2)}h}+\boldsymbol{b^{(2)}})$.

3.BP网络的学习方法

神经网络的关键之一是权值的确定，也即神经网络的学习，下面主要讨论一下BP神经网络的学习方法，它是一种监督学习的方法。
假定我们有$q$个带label的样本(即输入)$p_{1},p_{2},...,p_{q}$，对应的label(即期望输出Target)为$T_{1},T_{2},...,T_{q}$，神经网络的实际输出 为$a2_{1},a2_{2},...,a2_{q}$，隐层的输出为$a1[.]$那么可以定义误差函数：

$\boldsymbol{E(W,B)} = \frac{1}{2}\sum_{k=1}^{n}(t_{k} - a2_{k})^{2} $. BP算法的目标是使得实际输出approximate期望输出，即使得训练误差最小化。BP算法利用梯度下降(Gradient Descent)法来求权值的变化及 误差的反向传播。对于图1中的BP神经网络，我们首先计算输出层的权值的变化量，从第$i$个输入到第$k$个输出的权值改变为：
$\Delta w2_{ki} = - \eta \frac{\partial E}{\partial w2_{ki}} \\ = - \eta \frac{\partial E}{\partial a2_{k}} \frac{\partial a2_{k}}{\partial w2_{ki}} \\ = \eta (t_{k}-a2_{k})f_{2}'a1_{i} = \eta \delta_{ki}a1_{i}$. 其中$\eta$为学习速率。同理可得：
$\Delta b2_{ki} = - \eta \frac{\partial E}{\partial b2_{ki}} = - \eta \frac{\partial E}{\partial a2_{k}} \frac{\partial a2_{k}}{\partial b2_{ki}} = \eta (t_{k}-a2_{k})f_{2}' = \eta \delta_{ki}$. 而隐层的权值变化为：
$\Delta w1_{ij} = - \eta \frac{\partial E}{\partial w1_{ij}} = - \eta \frac{\partial E}{\partial a2_{k}} \frac{\partial a2_{k}}{\partial a1_{i}} \frac{\partial a1_{i}}{\partial w1_{ij}} = \eta \sum_{k=1}^{n}(t_{k}-a2_{k})f_{2}'w2_{ki}f_{1}'p_{j} = \eta \delta_{ij}p_{j}$. 其中，$\delta_{ij} = e_{i}f_{1}', e_{i} = \sum_{k=1}^{n}\delta_{ki}w2_{ki}$
同理可得，$\Delta b1_{i} = \eta \delta_{ij}$。
这里我们注意到，输出层的误差为$e_{j},j=1..n$，隐层的误差为$e_{i},i=1..m$，其中$e_{i}$可以认为是$e_{j}$的加权组合，由于作用函数的 存在，$e_{j}$的等效作用为$\delta_{ji} = e_{j}f'()$。

4.BP网络的设计

在进行BP网络的设计是，一般应从网络的层数、每层中的神经元个数和激活函数、初始值以及学习速率等几个方面来进行考虑，下面是一些选取的原则。

1.网络的层数
理论已经证明，具有偏差和至少一个S型隐层加上一个线性输出层的网络，能够逼近任何有理函数，增加层数可以进一步降低误差，提高精度，但同时也是网络 复杂化。另外不能用仅具有非线性激活函数的单层网络来解决问题，因为能用单层网络解决的问题，用自适应线性网络也一定能解决，而且自适应线性网络的 运算速度更快，而对于只能用非线性函数解决的问题，单层精度又不够高，也只有增加层数才能达到期望的结果。

2.隐层神经元的个数
网络训练精度的提高，可以通过采用一个隐含层，而增加其神经元个数的方法来获得，这在结构实现上要比增加网络层数简单得多。一般而言，我们用精度和 训练网络的时间来恒量一个神经网络设计的好坏：
（1）神经元数太少时，网络不能很好的学习，训练迭代的次数也比较多，训练精度也不高。
（2）神经元数太多时，网络的功能越强大，精确度也更高，训练迭代的次数也大，可能会出现过拟合(over fitting)现象。
由此，我们得到神经网络隐层神经元个数的选取原则是：在能够解决问题的前提下，再加上一两个神经元，以加快误差下降速度即可。

3.初始权值的选取
一般初始权值是取值在$(-1,1)$之间的随机数。另外威得罗等人在分析了两层网络是如何对一个函数进行训练后，提出选择初始权值量级为$\sqrt[r]{s}$的策略， 其中$r$为输入个数，$s$为第一层神经元个数。

4.学习速率
学习速率一般选取为$0.01 - 0.8$，大的学习速率可能导致系统的不稳定，但小的学习速率导致收敛太慢，需要较长的训练时间。对于较复杂的网络， 在误差曲面的不同位置可能需要不同的学习速率，为了减少寻找学习速率的训练次数及时间，比较合适的方法是采用变化的自适应学习速率，使网络在 不同的阶段设置不同大小的学习速率。

5.期望误差的选取
在设计网络的过程中，期望误差值也应当通过对比训练后确定一个合适的值，这个合适的值是相对于所需要的隐层节点数来确定的。一般情况下，可以同时对两个不同 的期望误差值的网络进行训练，最后通过综合因素来确定其中一个网络。

5.BP网络的局限性

BP网络具有以下的几个问题：
(1)需要较长的训练时间：这主要是由于学习速率太小所造成的，可采用变化的或自适应的学习速率来加以改进。
(2)完全不能训练：这主要表现在网络的麻痹上，通常为了避免这种情况的产生，一是选取较小的初始权值，而是采用较小的学习速率。
(3)局部最小值：这里采用的梯度下降法可能收敛到局部最小值，采用多层网络或较多的神经元，有可能得到更好的结果。

6.BP网络的改进

BP算法改进的主要目标是加快训练速度，避免陷入局部极小值等，常见的改进方法有带动量因子算法、自适应学习速率、变化的学习速率以及作用函数后缩法等。 动量因子法的基本思想是在反向传播的基础上，在每一个权值的变化上加上一项正比于前次权值变化的值，并根据反向传播法来产生新的权值变化。而自适应学习 速率的方法则是针对一些特定的问题的。改变学习速率的方法的原则是，若连续几次迭代中，若目标函数对某个权倒数的符号相同，则这个权的学习速率增加， 反之若符号相反则减小它的学习速率。而作用函数后缩法则是将作用函数进行平移，即加上一个常数。

7.BP网络实现异或

见参考文献[7]或Andrew Ng. 的ML公开课的第8讲。

另外BP算法的讲解及C++实现参见[4]。

参考文献

[1]An Introduction to Back-Propagation Neural Networks: http://www.seattlerobotics.org/encoder/nov98/neural.html
[2]Wiki - Backpropagation: http://en.wikipedia.org/wiki/Backpropagation
[3]Chapter 7 The backpropagation algorithm of Neural Networks - A Systematic Introduction by Raúl Rojas: http://page.mi.fu-berlin.de/rojas/neural/chapter/K7.pdf
[4]Back-propagation Neural Net - C++ 实现: http://www.codeproject.com/Articles/13582/Back-propagation-Neural-Net
[5]《Visual C++数字图像模式识别技术及工程实践》(第3章)，求实科技 张宏林
[6]《Matlab神经网络设置及应用》(第5章)，周品，清华大学出版社