基于能量的模型和波尔兹曼机

由于深度置信网络（Deep Belief Networks，DBN）是基于限制性玻尔兹曼机（Restricted Boltzmann Machines，RBM）的深层网络结构，所以本文重点讨论一下玻尔兹曼机（BM），以及它的学习算法——对比散度（Contrastive Divergence，CD）算法。在介绍BM前，我们首先介绍一下基于能量的模型（Energy Based Model，EBM），因为BM是一种特殊的EBM。

1. 基于能量的模型(EBM)

基于能量的模型是一种具有普适意义的模型，可以说它是一种模型框架，在它的框架下囊括传统的判别模型和生成模型，图变换网络(Graph-transformer Networks)，条件随机场，最大化边界马尔科夫网络以及一些流形学习的方法等。EBM通过对变量的每个配置施加一个有范围限制的能量来捕获变量之间的依赖关系。EBM有两个主要的任务，一个是推断(Inference)，它主要是在给定观察变量的情况，找到使能量值最小的那些隐变量的配置；另一个是学习(Learning)，它主要是寻找一个恰当的能量函数，使得观察变量的能量比隐变量的能量低。

基于能量的概率模型通过一个能量函数来定义概率分布，

$p(x) = \frac{e^{E(x)}}{Z}.$ ... ① 其中Z为规整因子， $Z = \sum _{x} e^{-E(x)}.$ ... ② 基于能量的模型可以利用使用梯度下降或随机梯度下降的方法来学习，具体而言，就是以训练集的负对数作为损失函数， $l(\theta,D) = -L(\theta,D) = - \frac{1}{N}\sum_{x^{(i)}\in D} log p(x^{(i)}).$ ... ③ 其中$\theta$为模型的参数，将损失函数对$\theta$求偏导， $\Delta = \frac{\partial l(\theta,D)}{\partial \theta} = - \frac{1}{N} \frac{\partial \sum log p(x^{(i)})}{\partial \theta}.$ ... ④ 即得到损失函数下降最快的方向。

包含隐单元的EBMs

在很多情况下，我们无法观察到样本的所有属性，或者我们需要引进一些没有观察到的变量，以增加模型的表达能力，这样得到的就是包含隐含变量的EBM，

$P(x) = \sum _{h} P(x,h) = \sum _{h} \frac{e^{-E(x,h)}}{Z}.$ ... ⑤ 其中$h$表示隐含变量。在这种情况下，为了与不包含隐含变量的模型进行统一，我们引入如下的自由能量函数， $F(x) = - log \sum_{h}e^{-E(x,h)}.$ ... ⑥ 这样$P(x)$就可以写成， $P(x) = \frac{e^{-F(x)}}{Z}, where Z = \sum_{x} e^{-F(x)}.$ ... ⑦ 此时，损失函数还是类似的定义，只是在进行梯度下降求解时稍微有些不同， $\Delta = - \frac{\partial log p(x)}{\partial \theta} = - \frac{\partial (-F(x) -log Z)}{\partial \theta} = \frac{\partial F(x)}{\partial \theta} - \sum_{\hat{x}} p(\hat{x}) \frac{\partial F(\hat{x})}{\partial \theta}$. ... ⑧ 该梯度表达式中包含两项，他们都影响着模型所定义的分布密度：第一项增加训练数据的概率（通过减小对应的自由能量），而第二项则减小模型生成的样本的概率。

通常，我们很难精确计算这个梯度，因为式中第一项涉及到可见单元与隐含单元的联合分布，由于归一化因子$Z(\theta)$的存在，该分布很难获取[3]。我们只能通过一些采样方法（如Gibbs采样）获取其近似值，其具体方法将在后文中详述。

2. 限制性玻尔兹曼机

玻尔兹曼机（Boltzmann Machine，BM）是一种特殊形式的对数线性的马尔科夫随机场（Markov Random Field，MRF），即能量函数是自由变量的线性函数。通过引入隐含单元，我们可以提升模型的表达能力，表示非常复杂的概率分布。

限制性玻尔兹曼机（RBM）进一步加一些约束，在RBM中不存在可见单元与可见单元的链接，也不存在隐含单元与隐含单元的链接，如下图所示

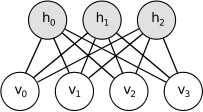
RBM的能量函数$E(v,h)$定义为， $E(v,h) = -b'v - c'h - h'Wv$. 其中'表示转置，$b,c,W$为模型的参数，$b,c$分别为可见层和隐含层的偏置，$W$为可见层与隐含层的链接权重。此时，对应的自由能量为， $F(v) = -b'v - \sum_{i}log\sum_{h_{i}}e^{h_{i}(c_{i}+W_{i}v)}.$ ... ⑨ 另外，由于RBM的特殊结构，可见层/隐含层内个单元之间是相互独立的，所以我们有， $p(h|v) = \prod _{i} p(h_{i}|v)$, $p(v|h) = \prod _{j} p(v_{j}|h).$ ... ⑩

使用二值单元的RBM

如果RBM中的每个单元都是二值的，即有$v_{j},h_{i} \in \{0,1\}$，我们可以得到，

$p(h_{i}=1|v) = sigmoid(c_{i} + W_{i}v)$, $p(v_{j}=1|h) = sigmoid(b_{j} + W_{j}'h).$ ... ⑪ 而对应的自由能量函数为， $F(v) = -b'v - \sum_{i}log(1+e^{c_{i}+W_{i}v}).$ ... ⑫ 使用梯度下降法求解模型参数时，各参数的梯度值如下[2]， $-\frac{\partial logp(v)}{\partial W_{ij}} = E_{v}[p(h_{i}|v) * v_{j}] - v_{j}^{(i)} * sigmoid(W_{i} * v^{(i)}+c_{i}),$ $-\frac{\partial logp(v)}{\partial c_{i}} = E_{v}[p(h_{i}|v) * v_{j}] - sigmoid(W_{i} * v^{(i)}),$ $-\frac{\partial logp(v)}{\partial b_{j}} = E_{v}[p(h_{i}|v) * v_{j}] - v_{j}^{(i)}.$ ... ⑬

3. RBM的学习

前面提到了，RBM是很难学习的，即模型的参数很难确定，下面我们就具体讨论一下基于采样的近似学习方法。学习RBM的任务是求出模型的参数 $\theta = \{c, b, W\}$的值。

3.1 Gibbs采样

Gibbs采样是一种基于马尔科夫链蒙特卡罗(Markov Chain Monte Carlo,MCMC)策略的采样方法。对于一个$K$为随机向量$X = (X_{1},X_{2},...,X_{K})$，假设我们无法求得关于$X$的联合分布$P(X)$，但我们知道给定$X$的其他分量时，其第$k$个分量$X_{k}$的条件分布，即$P(X_{k}|X_{k^{-}})$，其中$X_{k^{-}} = (X_{1},X_{2},...,X_{k-1},X_{k+1},...,X_{K})$，那么，我们可以从$X$的一个任意状态(比如[$x_{1}(0),x_{2}(0),...,x_{K}(0)$])开始，利用上述条件分布，迭代的对其分量依次采样，随着采样次数的增加，随机变量[$x_{1}(n),x_{2}(n),...,x_{K}(n)$]的概率分布将以$n$的几何级数的速度收敛于$X$的联合概率分布$P(X)$。也就是说，我们可以在未知联合概率分布的条件下对其进行采样。

基于RBM的对称结构，以及其中神经元状态的条件独立性，我们可以使用Gibbs采样方法得到服从RBM定义的分布的随机样本。在RBM中进行$k$步Gibbs采样的具体算法为：用一个训练样本(或可见层的任何随机化状态)初始化可见层的状态$v0$，交替进行如下采样：

$h_{0} \sim P(h|v_{0}), v_{1} \sim P(v|h_{0}),$ $h_{1} \sim P(h|v_{1}), v_{2} \sim P(v|h_{1}),$ $... ..., v_{k+1} \sim P(v|h_{k})$. 在经过步数$k$足够大的情况下，我们可以得到服从RBM所定义的分布的样本。此外，使用Gibbs采样我们也可以得到式⑧中第一项的近似。

3.2 对比散度算法

尽管利用Gibbs采样我们可以得到对数似然函数关于未知参数梯度的近似，但通常情况下需要使用较大的采样步数，这使得RBM的训练效率仍然不高，尤其是当观测数据的特征维数较高时。2002年，Hinton[4]提出了RBM的一个快速学习算法，即对比散度（Contrastive Divergence，CD）。与Gibbs采样不同，Hinton指出当使用训练数据初始化$v_{0}$时，我们仅需要使用$k$（通常k=1）步Gibbs采样变可以得到足够好的近似。在CD算法一开始，可见单元的状态被设置成一个训练样本，并利用式⑪第一个式子来计算所有隐层单元的二值状态，在所有隐层单元的状态确定了之后，根据式⑪第二个式子来确定第$i$个可见单元$v_{i}$取值为1的概率，进而产生可见层的一个重构 (reconstruction)。然后将重构的可见层作为真实的模型代入式⑬各式中第一项，这样就可以进行梯度下降算法了。

在RBM中，可见单元一般等于训练数据的特征维数，而隐层单元数需要事先给定，这里设可见单元数和隐单元数分别为$n$和$m$，令$W$表示可见层与隐层间的链接权重矩阵(m×n阶)，$a$(n维列向量)和$b$(m维列向量)分别表示可见层与隐层的偏置向量。RBM的基于CD的快速学习算法主要步骤如下：

//输入：一个训练样本x0; 隐层单元个数m; 学习率alpha; 最大训练周期T
//输出：链接权重矩阵W, 可见层的偏置向量a, 隐层的偏置向量b
//训练阶段
初始化：令可见层单元的初始状态v1 = x0; W, a, b为随机的较小数值
For t=1,2,...,T
  For j=1,2,...,m //对所有隐单元
      计算P(h1j=1|v1), 即P(h1j=1|v1) = sigmoid(bj+sum_i(v1i*Wij));
      从条件分布P(h1j|v1)中抽取h1j ∈ {0,1}
  EndFor
  
  For i=1,2,...,n //对所有可见单元
      计算P(v2i=1|h1), 即P(v2i=1|h1) = sigmoid(ai+sum_j(Wij*h1j));
      从条件分布P(v2i|h1)中抽取v2i ∈ {0,1}
  EndFor
  
  For j=1,2,...,m //对所有隐单元
      计算P(h2j=1|v2), 即P(h2j=1|v2) = sigmoid(bj+sum_i(v2i*Wij));
  EndFor
  
  //更新RBM的参数
  W = W + alpha *(P(h1=1|v1)v1' - P(h2=1|v2)v2');
  a = a + alpha *(v1-v2);
  b = b + alpha *(P(h1=1|v1) - P(h2=1|v2));
EndFor

上述基于CD的学习算法是针对RBM的可见单元和隐层单元均为二值变量的情形，我们可以很容易的推广到这些单元为高斯变量的情形。

RBM的完整实现参见https://github.com/ibillxia/DeepLearnToolbox/tree/master/DBN的Matlab代码。

References

[1] Learn Deep Architectures for AI, Chapter 5.
[2] Deep Learning Tutorial, Release 0.1, Chapter 9.
[3] 受限波尔兹曼机简介. 张春霞.
[4] Training Products of experts by minimizing contrastive divergence. GE Hinton.