语音信号处理之时域分析-音高追踪及其Python实现

| Comments

1.概述

在音高及其Python实现一文 中，我们使用了简单的“观察法”来计算音高，这并不太难，但这并不有好而且费时费力，那么我们就想，如何通过分析和计算，使用算法来自动计算音高呢？ 用算法让计算机自动抓取音高的过程，称为音高追踪(Pitch Tracking)。所得到的音高信息有如下一些应用：
·旋律识别(Melody Recognition)：或称为“哼唱选歌”，也就是如何由使用者的哼唱，找出音乐资料库中间对应的歌。
·汉语声调识别(Tone Recognition)：辨识使用者讲一句话时，每一个字的声调（一声、二声、三声、四声等）。
·语音合成韵律分析(Prosody Analysis)中的音高分析：如何在合成语音时，使用最自然的音高曲线。
·语音评分中的音调评分(Intonation Assessment)：如何评估使用者说话的语音，其音高曲线是否标准。
·语音识别(Speech Recognition)：我们可以使用语句的音高来提高语音辨识的正确率。
总而言之，音高追踪是语音信号处理中最基本也最重要的一个环节之一。

2.音高追踪的基本流程

音高追踪的基本流程如下：
(1)将整段音讯讯号切成音框（Frames），相邻音框之间可以重叠。
(2)算出每个音框所对应的音高。
(3)排除不稳定的音高值。（可由音量来筛选，或由音高值的范围来过滤。）
(4)对整段音高进行平滑化，通常是使用「中位数滤波器」（Median Filters）。

在切音框的过程中，我们允许左右音框的重叠，因此，我们定义「音框率」（Frame Rate）是每秒钟所出现的音框个数，如果取样频率是11025，音框长度是256 点， 重叠点数是84，那么音框率就是11025/(256-84) = 64，换句话说，我们的电脑要能够每秒钟处理64 个音框，才能达到实时处理的要求。如下图所示：

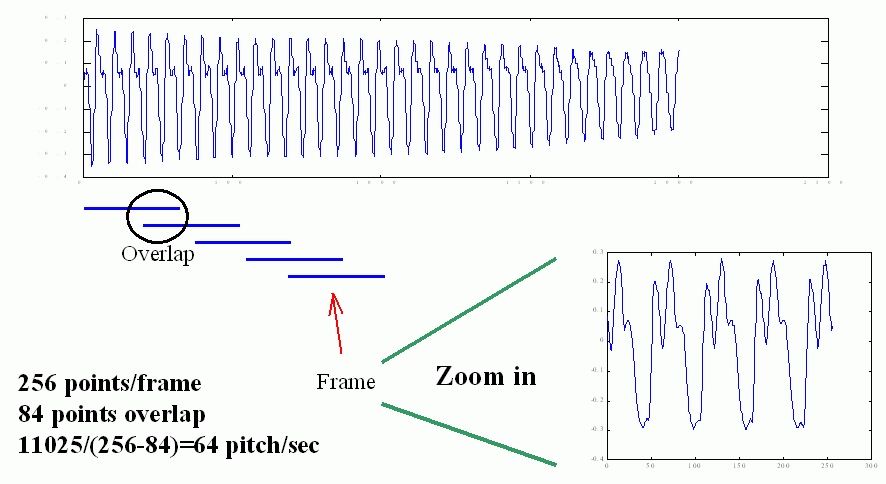
我们让音框重叠的目地，只是希望相邻音框之间的变化不会太大，使抓出来的音高曲线更具有连续性。但是在实际应用时，音框的重叠也不能太大， 否则会造成计算量的过大。一般有以下考虑：
·音框长度至少必须包含2 个基本周期以上，才能显示语音的特性。已知人声的音高范围大约在50 Hz 至1000 Hz 之间，因此对于一个的取样频率，我们就可以计算出 音框长度的最小值。例如，若取样频率fs = 8000 Hz，那么当音高f = 50 Hz（例如男低音的歌声）时，每个基本周期的点数是fs/f = 8000/50 = 160，因此音框必须 至少是320 点；若音高是1000 Hz（例如女高音的歌声）时，每个基本周期的点数是8000/1000 = 8，因此音框必须至少是16 点。
·音框长度也不能太大，太长的音框无法抓到音讯的特性随时间而变化的细微现象，同时计算量也会变大。
·音框之间的重叠完全是看计算机的运算能力来决定，若重叠多，音框率就会变大，计算量就跟着变大。若重叠少（甚至可以不重叠或跳点），音框率就会变小， 计算量也跟着变小。

3.音高追踪算法

3.1概述

由一个音框计算出音高的方法很多，可以分为时域和频域两大类：
时域（Time Domain）
·ACF: Autocorrelation function，自相关函数
·AMDF: Average magnitude difference function，平均强度差分函数
·SIFT: Simple inverse filter tracking
频域（Frequency Domain）
·Harmonic product spectrum method
·Cepstrum method

3.2 ACF自相关函数

首先，我们来看看ACF(Auto-Correlation Function，自相关函数)的概念。要计算音高，就得找出波形中的周期性，自相关函数的目的就是估算语音信号当前 帧与它的下一帧的相似性，其定义如下：

$acf(\tau) = \sum_{i=0}^{n-1-\tau}s(i)s(i+\tau)$
其中$\tau$是一个延迟的时间间隔。在某个区间使得$acf(\tau)$取得最大值的那个$\tau$值就选为pitch的起止点，如下图所示：
也就是说，我们将原始语音信号与其平移延迟信号的重叠（时间上重叠）部分进行内积运算，从而得到ACF。下面看一个具体的实例，其代码如下： ``` py3 import wave import numpy as np import pylab as pl def ACF(frame): flen = len(frame) acf = np.zeros(flen) for i in range(flen): acf[i] = np.sum(frame[i:flen]*frame[0:flen-i]) return acf # ============ test the algorithm ============= # read wave file and get parameters. fw = wave.open('a.wav','rb') params = fw.getparams() print(params) nchannels, sampwidth, framerate, nframes = params[:4] strData = fw.readframes(nframes) waveData = np.fromstring(strData, dtype=np.int16) waveData = waveData*1.0/max(abs(waveData)) # normalization fw.close() # plot the wave time = np.arange(0, len(waveData)) * (1.0 / framerate) frameSize = 512 idx1 = 10000 idx2 = idx1+frameSize index1 = idx1*1.0 / framerate index2 = idx2*1.0 / framerate acf = ACF(waveData[idx1:idx2]) #acf[0:10] = -acf[0] #acfmax = np.argmax(acf) #print(acfmax) #print(framerate*1.0/acfmax) pl.subplot(311) pl.plot(time, waveData) pl.plot([index1,index1],[-1,1],'r') pl.plot([index2,index2],[-1,1],'r') pl.xlabel("time (seconds)") pl.ylabel("Amplitude") pl.subplot(312) pl.plot(np.arange(frameSize),waveData[idx1:idx2],'r') pl.xlabel("index in 1 frame") pl.ylabel("Amplitude") pl.subplot(313) pl.plot(np.arange(frameSize),acf,'g') pl.xlabel("index in 1 frame") pl.ylabel("ACF") pl.show() ``` 程序运行结果如下图所示：

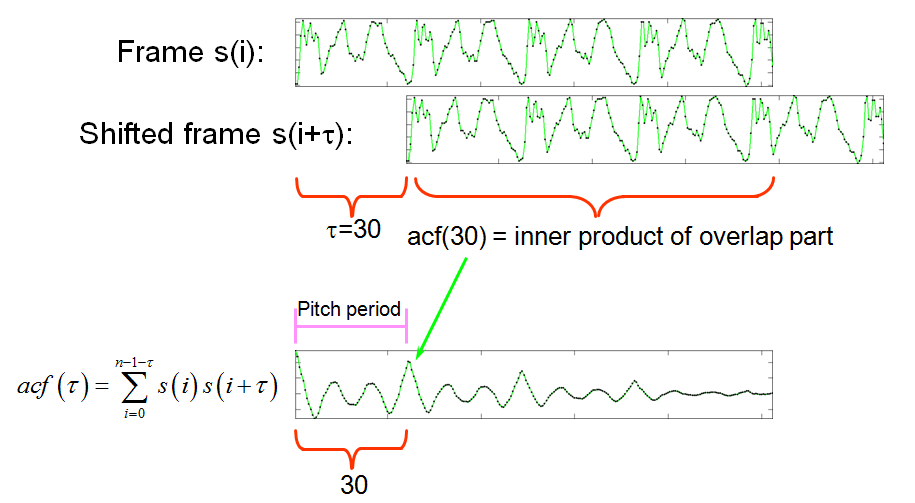
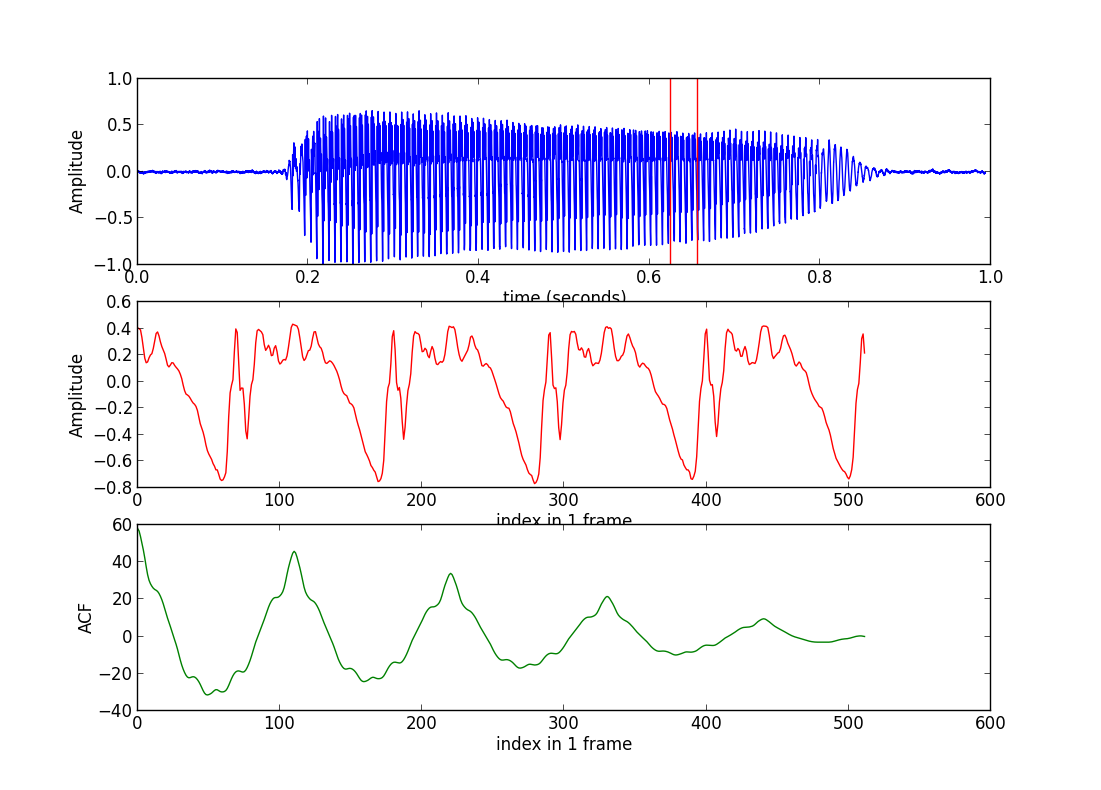
很显然，ACF的最大值出现在第一点，这一点作为起点在任何情况下都是已知的，我们需要知道是第二个波峰。我们可以将开始的一些点的ACF值设为负无穷（这里我 设为-acf[0]），这样可以找到第二个波峰的index为110（这一点称为pitch point，简称pp），那么对应的pitch为framerate/110 = 16000/110 = 145.455Hz.这个过程取消 程序中第32行起的4行注释即可。这样，我们就初步自动计算出了pitch了。

但是，细心的读者会发现，这里还有一个问题，那就是ACF曲线中前多少个点应该被置为负无穷？为简单起见，设人的pitch的范围为[40,1000](Hz)，那么pp的值应满足为： $40 < \frac{fs}{pp} < 1000$，从而得到pp的范围：$\frac{fs}{1000} < pp < \frac{fs}{40}$。这样可以部分解决问题，对于某些情况可能结果并不一定正确。

另外还有一些对ACF的改进。一个主要的改进原因是，当$\tau$值变大是，两端信号的重叠部分逐渐变小，这样计算出来的ACF当然越来越小。一种改进是增加一个权值：

$acf(\tau) = \sum_{i=0}^{n-1-\tau} \frac{s(i)s(i+\tau)}{n-\tau}$.
这种方法虽然解决了上面提到的问题，但又引入了一个新的问题，那就是，在$\tau$值较大时，计算出来的acf和pitch的差异可能很大，也即出现了不稳定。另一种改进是， 将$\tau$限制在半帧内，也即：
$acf(\tau) = \sum_{i=0}^{n/2}s(i)s(i+\tau)$.
但这样得到的acf只有一帧的一半，对于音高较低的信号就不利了，这时我们就得增大帧的长度，于是计算量也相应的增加了。

3.3 NSDF

ACF的范围是未知的，NSDF(normalized squared difference function)将ACF规整到[-1,1]之间，其定义的表达式如下：

$nsdf(\tau) = \frac{2\sum s(i)s(i+\tau)}{\sum s^{2}(i) + \sum s^{2}(i+\tau)}$.

3.4 AMDF

AMDF (average magnitude difference function) 的定义如下：

$amdf(\tau) = \sum_{i=0}^{n-1-\tau}|s(i)-s(i+\tau)|$.
与ACF相反，这里用距离而不是相似度来计算，所以这里选取pitch point(简称pp)的标准是选最小值对应的index(实际代码中，为了与ACF进行统一，我对AMDF取了相反数)。 相应的，也有一些对AMDF这个函数的修正，如加权值、只是用前半帧等，另外还可以将AMDF与ACF结合，将ACF除以AMDF，得到的结果可以更容易找到pitch point。

3.5 Pitch Tracking

能够正确计算pitch了，我们就可以对一段时序的信号进行pitch tracking了。

PS：另外，还有一些频域的音高追踪方法，将在后续文章中介绍。

4.参考资料

[1]Audio Signal Processing and Recognition, Chap 7: http://neural.cs.nthu.edu.tw/jang/books/audiosignalprocessing/index.asp